Geometria Espacial na Prova do ENEM
A Geometria Espacial é um dos tópicos fundamentais na prova de matemática do ENEM e é crucial para a compreensão de diversos problemas envolvendo formas tridimensionais. Saber lidar com volumes, áreas de superfícies e propriedades de figuras espaciais é essencial para resolver questões que exigem uma boa visualização e compreensão espacial. Neste post, vamos explorar os conceitos principais de Geometria Espacial e como eles aparecem na prova do ENEM, oferecendo dicas valiosas para que você possa se preparar de forma eficiente. Confira, no final deste post, nossa lista de exercícios das provas anteriores, selecionados de acordo com a dificuldade da questão e feita especialmente para você. Boa leitura e bons estudos.

Conceitos Básicos
A Geometria Espacial estuda figuras em três dimensões, como cubos, paralelepípedos, cilindros, cones, esferas e prismas. Diferente da geometria plana, que lida com figuras em duas dimensões (como quadrados e círculos), a geometria espacial requer a compreensão de volume e área de superfícies. Entender essas propriedades é fundamental, pois muitas questões do ENEM exigem cálculos precisos de volume e área, além de uma boa visualização das figuras.
Volumes
O cálculo de volumes é uma parte crucial da Geometria Espacial. Cada tipo de sólido tem uma fórmula específica para o cálculo do volume. Por exemplo, o volume de um cubo, volume de cilindro, etc. Saber as fórmulas e como aplicá-las é essencial para resolver questões do ENEM que envolvem o cálculo de volumes de diferentes sólidos.
Áreas de Superfícies
Além dos volumes, a Geometria Espacial também envolve o cálculo das áreas das superfícies dos sólidos. O ENEM frequentemente inclui questões que exigem o cálculo da área total ou da área de superfícies específicas dos sólidos, sendo fundamental conhecer essas fórmulas e saber aplicá-las corretamente.
Aplicações Práticas no ENEM
No ENEM, questões de Geometria Espacial aparecem frequentemente em contextos práticos, como problemas envolvendo embalagens, construção civil e projetos arquitetônicos. Por exemplo, você pode encontrar uma questão que pede para calcular o volume de uma caixa d’água ou a quantidade de material necessário para cobrir uma superfície. Resolver esses problemas requer não só o conhecimento das fórmulas, mas também a capacidade de interpretar e aplicar essas informações em situações do dia a dia.
O que mais cai sobre Geometria Espacial? (2014 – 2023)
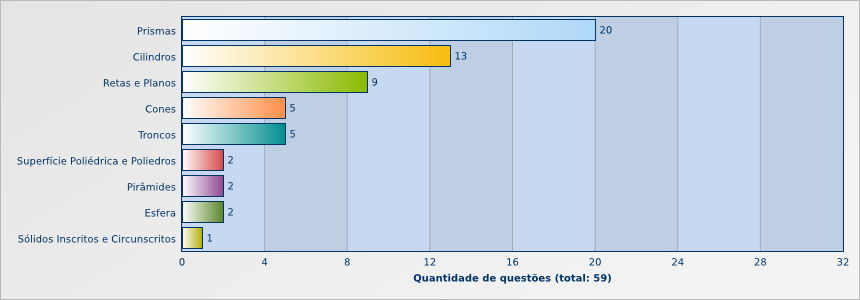
Estratégias de Estudo
Para se preparar bem para o ENEM, é essencial praticar com exercícios que envolvem Geometria Espacial. Resolver questões de provas anteriores e simulados ajuda a familiarizar-se com o estilo das perguntas e a identificar rapidamente o tipo de sólido e as fórmulas necessárias. Além disso, estudar diferentes aplicações práticas, como problemas de construção e design, pode reforçar a compreensão do conceito e melhorar a habilidade de resolver problemas de forma eficiente.
Revisão de Conceitos Básicos
Por fim, revisar conceitos básicos de geometria plana, como áreas e perímetros, é crucial para lidar com Geometria Espacial. Muitas vezes, as questões exigem uma combinação desses conhecimentos para chegar à resposta correta. Manter um estudo regular e variado, focando em diferentes tipos de problemas e suas aplicações, pode fazer toda a diferença no desempenho na prova.
Conclusão
Em resumo, a Geometria Espacial é um tema chave na prova de matemática do ENEM e aparece em diversas formas e contextos. Entender volumes e áreas de superfícies, saber aplicar as fórmulas corretamente e praticar com exercícios variados são passos essenciais para garantir um bom desempenho. Com dedicação e prática, você estará bem preparado para enfrentar essas questões com confiança.

