Funções na Prova do ENEM
As Funções são um dos tópicos fundamentais na prova de matemática do ENEM e desempenham um papel crucial na modelagem de relações entre variáveis. Compreender os conceitos de funções, seus diferentes tipos e aplicações é essencial para resolver questões que envolvem análise de dados, interpretação de gráficos e resolução de problemas do mundo real. Neste post, vamos explorar os principais aspectos das funções e como elas aparecem na prova do ENEM, oferecendo dicas valiosas para que você possa se preparar de forma eficiente. Confira, no final deste post, nossa lista de exercícios das provas anteriores, selecionados de acordo com a dificuldade da questão e feita especialmente para você. Boa leitura e bons estudos.

Conceitos Básicos
Uma função é uma relação matemática entre dois conjuntos de números, onde cada elemento do primeiro conjunto (domínio) está associado a exatamente um elemento do segundo conjunto (contradomínio). As funções podem ser representadas de diversas formas, como por meio de equações, tabelas, gráficos e até mesmo verbalmente. É importante compreender conceitos como domínio, contradomínio, imagem e conjunto solução, além de saber identificar e interpretar diferentes representações de funções.
Tipos de Funções
No ENEM, é comum encontrar questões que envolvem diferentes tipos de funções, como funções lineares, quadráticas, exponenciais, logarítmicas e trigonométricas. Cada tipo de função tem características específicas e aplicações distintas. Por exemplo, funções lineares descrevem relações proporcionais e são representadas por retas, enquanto funções quadráticas descrevem parábolas e são frequentemente utilizadas para modelar fenômenos físicos.
Gráficos e Interpretações
Uma habilidade importante para resolver questões de funções no ENEM é a interpretação de gráficos. Os gráficos de funções fornecem informações visuais sobre o comportamento da função, como sua concavidade, pontos de máximo e mínimo, e comportamento assintótico. Além disso, é essencial compreender como diferentes parâmetros afetam o formato do gráfico, como a inclinação e a posição em relação aos eixos coordenados.
Aplicações Práticas no ENEM
As funções têm diversas aplicações práticas no ENEM, como em problemas de otimização, análise de crescimento populacional, modelagem de fenômenos físicos e econômicos, entre outros. Por exemplo, uma questão pode exigir a modelagem de um problema de movimento com uma função quadrática, ou a análise de dados utilizando uma função exponencial para prever o crescimento de uma população ao longo do tempo.
O que mais cai sobre Funções? (2014 – 2023)
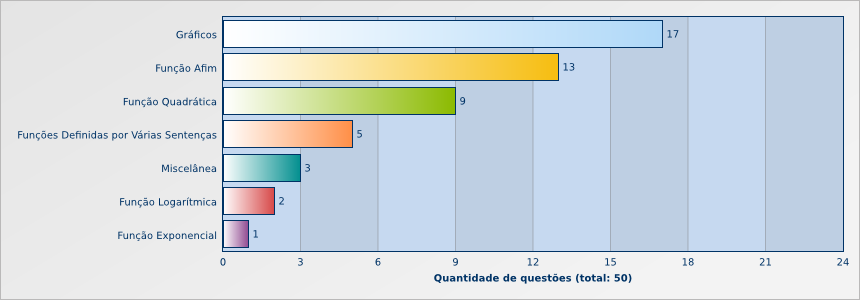
Estratégias de Estudo
Para se preparar bem para o ENEM, é essencial praticar com exercícios que envolvem funções. Resolver questões de provas anteriores e simulados ajuda a familiarizar-se com o estilo das perguntas e a identificar rapidamente o tipo de função envolvida. Além disso, estudar diferentes aplicações práticas, como problemas de interpretação de gráficos e modelagem de situações reais, pode reforçar a compreensão do conceito e melhorar a habilidade de resolver problemas de forma eficiente.
Revisão de Conceitos Básicos
Por fim, revisar conceitos básicos de matemática, como operações com números reais e resolução de equações, é crucial para lidar com funções no ENEM. Muitas vezes, as questões exigem uma combinação desses conhecimentos para chegar à resposta correta. Manter um estudo regular e variado, focando em diferentes tipos de funções e suas aplicações, pode fazer toda a diferença no desempenho na prova.
Conclusão
Em resumo, as funções são um tema chave na prova de matemática do ENEM e aparecem em diversas formas e contextos. Entender os conceitos básicos, os diferentes tipos de funções, saber interpretar gráficos e praticar com exercícios variados são passos essenciais para garantir um bom desempenho. Com dedicação e prática, você estará bem preparado para enfrentar essas questões com confiança.

